
 Ph.D. Student
Ph.D. StudentHi, thank you for stopping by my website
I earned my B.S. in Computer Science from the University of Engineering and Technology (UET), Vietnam National University in 2021, where I ranked in the top 1% of my cohort.
I'm pursuing a Ph.D. in Computer Science at North Carolina State University, advised by Dr. Jianqing Liu. My research focuses on quantum sensing, quantum networking, and the design of quantum algorithms for combinatorial problems. Along the way, I have received the Outstanding PhD Student Award and student travel grants from the National Science Foundation (NSF).
Warning
Problem: The current name of your GitHub Pages repository ("Solution: Please consider renaming the repository to "
http://".
However, if the current repository name is intended, you can ignore this message by removing "{% include widgets/debug_repo_name.html %}" in index.html.
Action required
Problem: The current root path of this site is "baseurl ("_config.yml.
Solution: Please set the
baseurl in _config.yml to "Education
-
 North Carolina State UniversityDepartment of Computer Science
North Carolina State UniversityDepartment of Computer Science
Ph.D. StudentAug. 2024 - present -
 VNU University of Engineering and Technology (VNU-UET)B.S. in Computer ScienceAug. 2017 - Aug. 2021
VNU University of Engineering and Technology (VNU-UET)B.S. in Computer ScienceAug. 2017 - Aug. 2021
Honors & Awards
-
Los Alamos Quantum Computing Summer School Fellowship (2% Acceptance Rate)2025
-
Quantum Leap Career Nexus Travel Grant ($600)2024
-
IEEE International Conference on Communications (ICC) NSF Travel Grant ($1,000)2024
-
IEEE International Conference on Communications (ICC) NSF Travel Grant ($1,200)2023
-
KSU College of Computing and Engineering Student Travel Grant ($1,500)2023
-
KSU Outstanding Ph.D. Student – Research Award2023
-
UET-FIT Dean’s list scholarships (6/8 semesters, $4000)2017-2021
News
Selected Publications (view all )
Partition Function Estimation Using Analog Quantum Processors
Thinh Le, Elijah Pelofske
Submitted to Nature Unconventional ComputingUnder review. 2025
We evaluate using programmable superconducting flux qubit D-Wave quantum annealers to approximate the partition function of Ising models. We propose the use of two distinct quantum annealer sampling methods: chains of Monte Carlo-like reverse quantum anneals, and standard linear-ramp quantum annealing. The control parameters used to attenuate the quality of the simulations are the effective analog energy scale of the J coupling, the total annealing time, and for the case of reverse annealing the anneal-pause. The core estimation technique is to sample across the energy spectrum of the classical Hamiltonian of interest, and therefore obtain a density of states estimate for each energy level, which in turn can be used to compute an estimate of the partition function with some sampling error. This estimation technique is powerful because once the distribution is sampled it allows thermodynamic quantity computation at arbitrary temperatures. On a $25$ spin $\pm J$ hardware graph native Ising model we find parameter regimes of the D-Wave processors that provide comparable result quality to two standard classical Monte Carlo methods, Multiple Histogram Reweighting and Wang-Landau. Remarkably, we find that fast quench-like anneals can quickly generate ensemble distributions that are very good estimates of the true partition function of the classical Ising model; on a Pegasus graph-structured QPU we report a logarithmic relative error of $7.6 \times 10^{-6}$, from $171,000$ samples generated using $0.2$ seconds of QPU time with an anneal time of $8$ nanoseconds per sample which is interestingly within the closed system dynamics timescale of the superconducting qubits.
Partition Function Estimation Using Analog Quantum Processors
Thinh Le, Elijah Pelofske
Submitted to Nature Unconventional ComputingUnder review. 2025
We evaluate using programmable superconducting flux qubit D-Wave quantum annealers to approximate the partition function of Ising models. We propose the use of two distinct quantum annealer sampling methods: chains of Monte Carlo-like reverse quantum anneals, and standard linear-ramp quantum annealing. The control parameters used to attenuate the quality of the simulations are the effective analog energy scale of the J coupling, the total annealing time, and for the case of reverse annealing the anneal-pause. The core estimation technique is to sample across the energy spectrum of the classical Hamiltonian of interest, and therefore obtain a density of states estimate for each energy level, which in turn can be used to compute an estimate of the partition function with some sampling error. This estimation technique is powerful because once the distribution is sampled it allows thermodynamic quantity computation at arbitrary temperatures. On a $25$ spin $\pm J$ hardware graph native Ising model we find parameter regimes of the D-Wave processors that provide comparable result quality to two standard classical Monte Carlo methods, Multiple Histogram Reweighting and Wang-Landau. Remarkably, we find that fast quench-like anneals can quickly generate ensemble distributions that are very good estimates of the true partition function of the classical Ising model; on a Pegasus graph-structured QPU we report a logarithmic relative error of $7.6 \times 10^{-6}$, from $171,000$ samples generated using $0.2$ seconds of QPU time with an anneal time of $8$ nanoseconds per sample which is interestingly within the closed system dynamics timescale of the superconducting qubits.
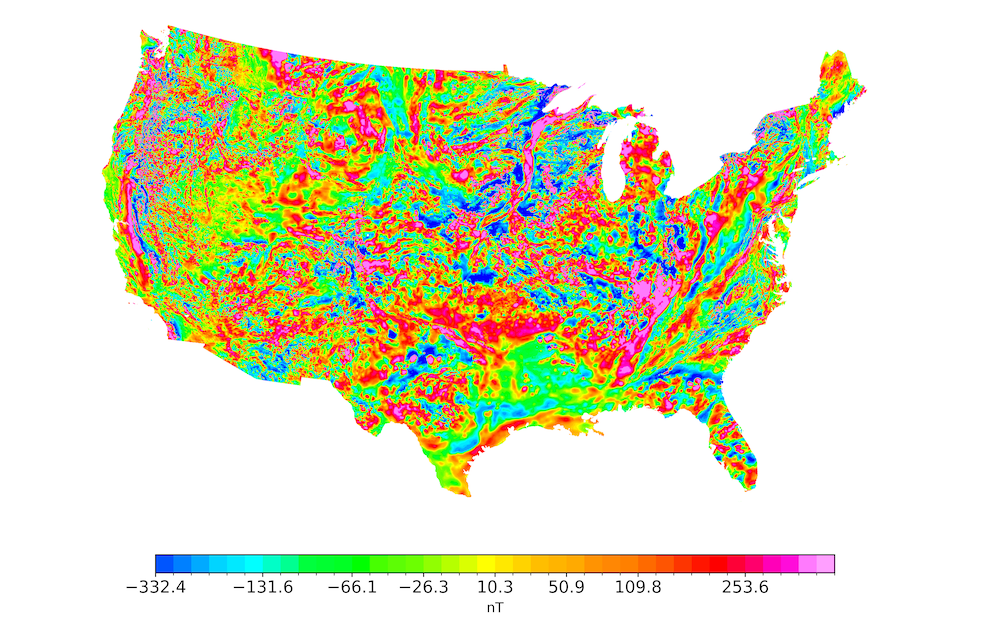
Distributed Quantum Magnetic Sensing for Infrastructure-free Geo-localization
Thinh Le, Jianqing Liu, Jiapeng Zhao, Eneet Kaur
Submitted to IEEE Transactions on NetworkingUnder review. 2025
Modern navigation systems rely heavily on Global Navigation Satellite Systems (GNSS), whose weak spaceborne signals are vulnerable to jamming, spoofing, and line-of-sight blockage. As an alternative, the Earth's magnetic field entails location information and is found critical to many animals' cognitive and navigation behavior. However, the practical use of the Earth's magnetic field for geo-localization hinges on an ultra-sensitive magnetometer. This work investigates how quantum magnetic sensing can be used for this purpose. We theoretically derive the Cramér--Rao lower bound (CRLB) for the estimation error of quantum sensing when using a nitrogen-vacancy (NV) center and prove the quantum advantage over classical magnetometers. Moreover, we employ a practical distributed quantum sensing protocol to saturate CRLB. Based on the estimated magnetic field and the earth's magnetic field map, we formulate geo-localization as a map-matching problem and introduce a coarse-to-fine Mahalanobis distance search in both gradient space (local field derivatives) and corner space (raw field samples). We simulate the proposed quantum sensing-based geo-localization framework over four cities in the United States and Canada. The results report that in high-gradient regions, gradient-space Mahalanobis search achieves sub-kilometer median localization error; while in magnetically smoother areas, corner-space search provides better accuracy and a $4-8\times$ reduction in runtime.
Distributed Quantum Magnetic Sensing for Infrastructure-free Geo-localization
Thinh Le, Jianqing Liu, Jiapeng Zhao, Eneet Kaur
Submitted to IEEE Transactions on NetworkingUnder review. 2025
Modern navigation systems rely heavily on Global Navigation Satellite Systems (GNSS), whose weak spaceborne signals are vulnerable to jamming, spoofing, and line-of-sight blockage. As an alternative, the Earth's magnetic field entails location information and is found critical to many animals' cognitive and navigation behavior. However, the practical use of the Earth's magnetic field for geo-localization hinges on an ultra-sensitive magnetometer. This work investigates how quantum magnetic sensing can be used for this purpose. We theoretically derive the Cramér--Rao lower bound (CRLB) for the estimation error of quantum sensing when using a nitrogen-vacancy (NV) center and prove the quantum advantage over classical magnetometers. Moreover, we employ a practical distributed quantum sensing protocol to saturate CRLB. Based on the estimated magnetic field and the earth's magnetic field map, we formulate geo-localization as a map-matching problem and introduce a coarse-to-fine Mahalanobis distance search in both gradient space (local field derivatives) and corner space (raw field samples). We simulate the proposed quantum sensing-based geo-localization framework over four cities in the United States and Canada. The results report that in high-gradient regions, gradient-space Mahalanobis search achieves sub-kilometer median localization error; while in magnetically smoother areas, corner-space search provides better accuracy and a $4-8\times$ reduction in runtime.
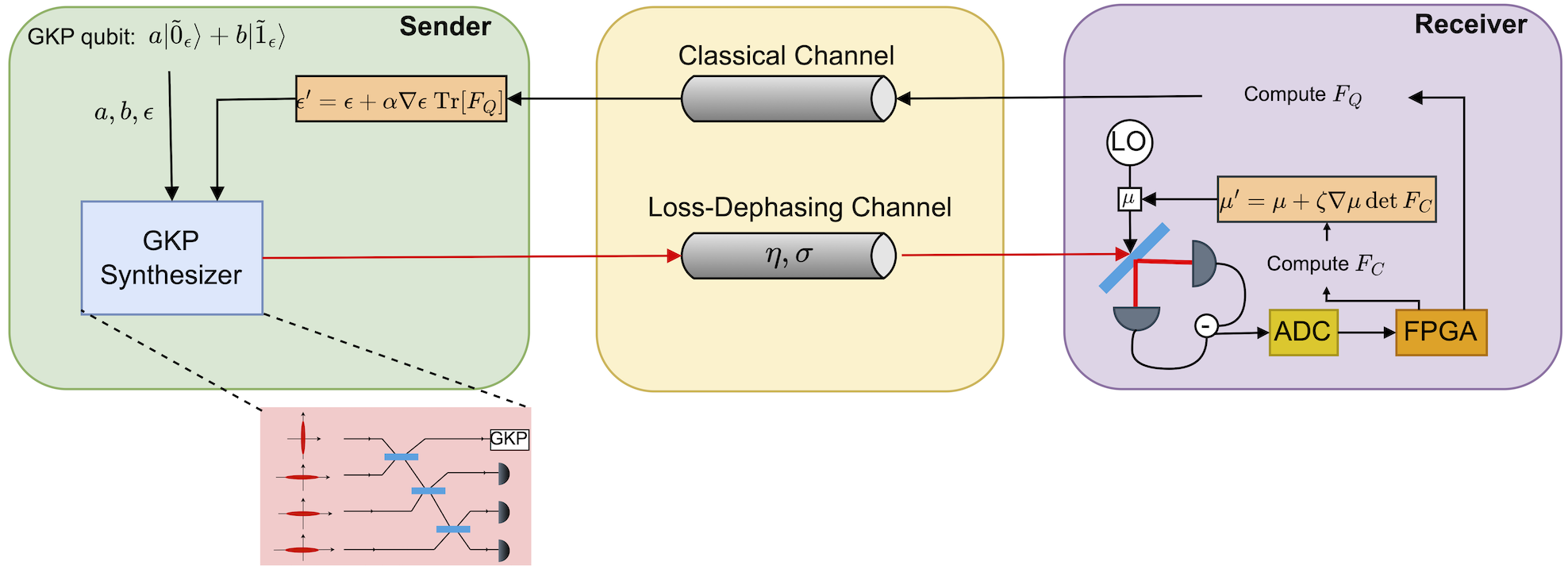
Optimized GKP State for Bosonic Channel Sensing
Thinh Le, Jianqing Liu, Jiapeng Zhao, Eneet Kaur
IEEE International Conference on Quantum Computing and Engineering (QCE'25) 2025
Bosonic quantum computation harnesses the infinite-dimensional Hilbert space of harmonic oscillators, offering scalable architectures with inherent error correction advantages over qubit-based systems. Despite their potential, bosonic modes encounter significant challenges from prevalent noise sources, particularly photon loss and dephasing, which degrade quantum coherence. Among bosonic error-correcting codes, the Gottesman-Kitaev-Preskill (GKP) code stands out for its ability to correct small phase-space displacements, enabling applications in quantum communication, sensing, and computation. While ideal GKP states require infinite squeezing and are unphysical, the finite squeezing approximate GKP states have been experimentally realized, though their performance depends critically on the squeezing level and measurement strategies. This work addresses a central challenge: how to optimize the squeezing parameter of approximate GKP states and the local oscillator (LO) phase in homodyne detection to maximize precision in estimating bosonic loss-dephasing channel parameters. To address this question, we introduce an adaptive optimization framework guided by classical Fisher information (CFI) and quantum Fisher information (QFI). Numerical simulations demonstrate that this adaptive protocol consistently converges to optimal parameter configurations, determining optimized squeezing levels and LO phases. By offering a practical approach to high-precision quantum channel parameter estimation, this framework has broad implications, from quantum metrology to enabling robust quantum communication systems.
Optimized GKP State for Bosonic Channel Sensing
Thinh Le, Jianqing Liu, Jiapeng Zhao, Eneet Kaur
IEEE International Conference on Quantum Computing and Engineering (QCE'25) 2025
Bosonic quantum computation harnesses the infinite-dimensional Hilbert space of harmonic oscillators, offering scalable architectures with inherent error correction advantages over qubit-based systems. Despite their potential, bosonic modes encounter significant challenges from prevalent noise sources, particularly photon loss and dephasing, which degrade quantum coherence. Among bosonic error-correcting codes, the Gottesman-Kitaev-Preskill (GKP) code stands out for its ability to correct small phase-space displacements, enabling applications in quantum communication, sensing, and computation. While ideal GKP states require infinite squeezing and are unphysical, the finite squeezing approximate GKP states have been experimentally realized, though their performance depends critically on the squeezing level and measurement strategies. This work addresses a central challenge: how to optimize the squeezing parameter of approximate GKP states and the local oscillator (LO) phase in homodyne detection to maximize precision in estimating bosonic loss-dephasing channel parameters. To address this question, we introduce an adaptive optimization framework guided by classical Fisher information (CFI) and quantum Fisher information (QFI). Numerical simulations demonstrate that this adaptive protocol consistently converges to optimal parameter configurations, determining optimized squeezing levels and LO phases. By offering a practical approach to high-precision quantum channel parameter estimation, this framework has broad implications, from quantum metrology to enabling robust quantum communication systems.